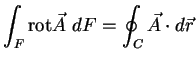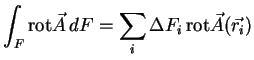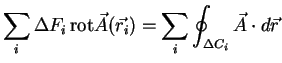Veranschaulichung des Gauß'schen und Stokes'schen
Satzes
Der Gauß'sche und der Stokes'sche Satz für Vektorfelder sind in
der Elektrodynamik unverzichtbar. Sie stellen ein Werkzeug zur Verfügung,
das den Umgang mit den Maxwell'schen Gleichungen erheblich erleichtert. Der
Gauß'sche Satz stellt eine Relation zwischen einem Vektorfeld
und seiner
Divergenz dar, der Stokes'sche Satz tut dies für die Rotation.
Zuerst sei die Divergenz eines Vektorfeldes als Skalarfeld folgendermaßen
definiert:
Es wird also über die Oberfläche 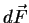 eines Volumenelementes
eines Volumenelementes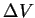 am Orte
am Orte 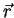 das Skalarprodukt
das Skalarprodukt 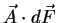 aufsummiert. Die Divergenz ist ein Maß für die Quellen-und Senkenstärke
eines Vektorfeldes (siehe auch Applet nebenan).
aufsummiert. Die Divergenz ist ein Maß für die Quellen-und Senkenstärke
eines Vektorfeldes (siehe auch Applet nebenan).
Die Rotation eines Vektorfeldes ist wieder ein Vektorfeld. Dabei
ist die
Komponente des Vektorfeldes in Richtung eines beliebigen Einheitsvektors 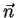 definiert durch:
definiert durch:
Über ein Flächenelement 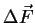 parallel zu
parallel zu 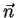 ander Stelle
ander Stelle 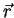 mit einem Rand
mit einem Rand 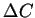 wird hier das Skalarprodukt
wird hier das Skalarprodukt 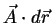 summiert.
summiert.
Der Gauß'sche Satz
Der Gauß'sche Satz besagt nun folgendes:
Anschaulich heißt das, dass der Anteil eines Vektorfeldes, der durch
die Oberfläche des Volumens 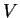 strömt, aus den Quellen im Volumen
strömt, aus den Quellen im Volumen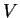 gekommen sein muss bzw. in den Senken des Volumens verschwindet.
gekommen sein muss bzw. in den Senken des Volumens verschwindet.
Nun muß der Satz aber noch bewiesen werden: Es sei das Volumen 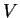 in kleine Teilvolumina
in kleine Teilvolumina 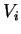 aufgeteilt. So gilt:
aufgeteilt. So gilt:
Führt man die letzte Summation tatsächlich aus, so werden wie im
Applet sichtbar die inneren Seiten der Teilvolumina im Inneren des Volumens
so aufsummiert, dass deren Vektoren
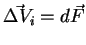 (im Applet rot, grün und blau) antiparallel stehen und sich daher diese
inneren Flächen wegheben.
Übrig bleibt somit nur die ,,Außenhaut''
des großen Volumens, also dessen Oberfläche. Also ist
Nach dem Grenzübergang von den diskreten, endlichen Flächenelementen
(im Applet rot, grün und blau) antiparallel stehen und sich daher diese
inneren Flächen wegheben.
Übrig bleibt somit nur die ,,Außenhaut''
des großen Volumens, also dessen Oberfläche. Also ist
Nach dem Grenzübergang von den diskreten, endlichen Flächenelementen
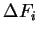 zu infinitesimal kleinen Flächen, erhält man so denGauß'schen
Satz, wie er oben vorweggenommen wurde.
zu infinitesimal kleinen Flächen, erhält man so denGauß'schen
Satz, wie er oben vorweggenommen wurde.
Der Stokes'sche Satz
Der Stokes'sche Satz ist dem Gauß'schen ähnlich:
Hier wird das Integral einer Rotation eines Vektorfeldes über eine
Fläche in ein Integral des Vektorfeldes selbst über den Rand dieser
Fläche überführt. Auch beim Beweis geht man ganz ähnlich vor: Sei
die Fläche 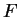 in kleine Teilflächen
in kleine Teilflächen
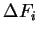 aufgeteilt, so gilt:
Bei der Summation werden wie im Applet
sichtbar die inneren Seiten der Teilflächen im Inneren der Fläche
so aufsummiert, dass deren innere Wege (im Applet gestrichelt mit
roten, grünen, orangenen und blauen Pfeilen) sich aufheben. Übrig
bleibt so wieder nur die ,,Außenhaut'' des Fläche, also deren Rand. Also ist
Nach dem Grenzübergang von den diskreten, endlichen Flächen- und Wegelementen
aufgeteilt, so gilt:
Bei der Summation werden wie im Applet
sichtbar die inneren Seiten der Teilflächen im Inneren der Fläche
so aufsummiert, dass deren innere Wege (im Applet gestrichelt mit
roten, grünen, orangenen und blauen Pfeilen) sich aufheben. Übrig
bleibt so wieder nur die ,,Außenhaut'' des Fläche, also deren Rand. Also ist
Nach dem Grenzübergang von den diskreten, endlichen Flächen- und Wegelementen
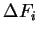 bzw
bzw
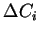 zu infinitesimal kleinen Flächen
und Wegen, bekommt man den Stokes'schen Satz, wie er oben angegeben wurde.
zu infinitesimal kleinen Flächen
und Wegen, bekommt man den Stokes'schen Satz, wie er oben angegeben wurde.
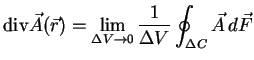
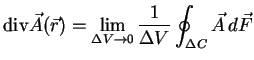
![]() definiert durch:
definiert durch:
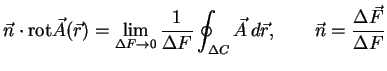
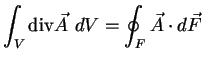
![]() in kleine Teilvolumina
in kleine Teilvolumina ![]() aufgeteilt. So gilt:
aufgeteilt. So gilt:
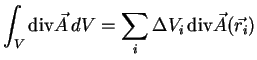
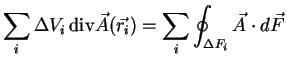
 zu infinitesimal kleinen Flächen, erhält man so denGauß'schen
Satz, wie er oben vorweggenommen wurde.
zu infinitesimal kleinen Flächen, erhält man so denGauß'schen
Satz, wie er oben vorweggenommen wurde.