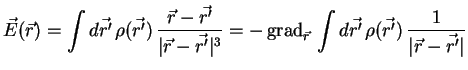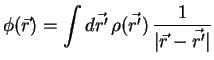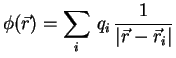Applet für E-Felder von Multipolen
elektrische Felder von Ladungsverteilungen
Eine kleine Anleitung
physikalischer Hintergrund
Das elektrische Feld einer beliebigen Ladungsverteilung
 ist durch
gegeben, wobei
ist durch
gegeben, wobei
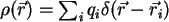 ist. Setzt man dies in die Gleichung für das elektrische Feld ein, so
ergibt sich
ist. Setzt man dies in die Gleichung für das elektrische Feld ein, so
ergibt sich
Dies ist nun das elektrische Feld, das oben im Applet sichbar gemacht
wird. Dabei sind die mit i indizierten r's die Orte der Ladungen und
das ,,normale'' r die Rasterpunkte, an denen das E-Feld ausgewertet
wird.
Aus dem elektrischen Feld läßt sich über die Beziehung
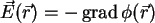 das Potential
das Potential 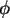 herleiten:
herleiten:
Hierbei wurde die Beziehung
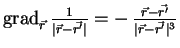 verwendet. Also
ist
Mit der oben gegebenen Ladungsverteilung folgt daraus dann
verwendet. Also
ist
Mit der oben gegebenen Ladungsverteilung folgt daraus dann
Erstellt von Philipp Koch
Universität Konstanz - Lehrstuhl Nielaba
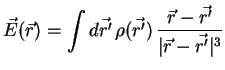
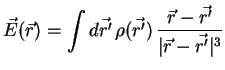
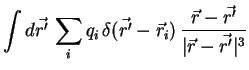
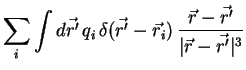
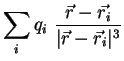
![]() das Potential
das Potential ![]() herleiten:
herleiten: